Home Page or Table of Contents
The use of Fourier transforms to convert raw SAR imagery data into a pictorial radar "scene" can be looked upon as a computational short-cut to perform the same operations as the "brute-force approach" accomplishes ( see SAR Processing (Brute Force, Single Range Bin)) . The short-cut can be thought of as a means of accomplishing either vector rotation or cross-correlation (see Ways of Interpreting the Fourier Transform).
The "brute-force approach" provides a true radar image in the sense that every range line is on boresight -- that is, the end effects in the Doppler (or azimuthal) direction are the same for every range line which is computed. In using Fourier transforms, however, only one range line is truly on boresight -- namely the range line in the center of the transform as computed from negative to positive Doppler (right to left azimuth). Nevertheless, off-boresight effects can be minimized to the point that the visual image produced by a Fourier transform is difficult to distinguish from that produced by the "brute-force approach," and the computational savings are significant.
The one-dimensional Fourier transform approach can be thought of as a means of performing Doppler correlation with range correction. The Doppler history in a single range bin is illustrated below, where the maximum positive Doppler occurs at the beginning of the approach towards the range bin of interest, the zero Doppler point occurs broadside to the range bin of interest (on boresight), and the maximum negative Doppler occurs at the end of the recession from the range bin of interest:
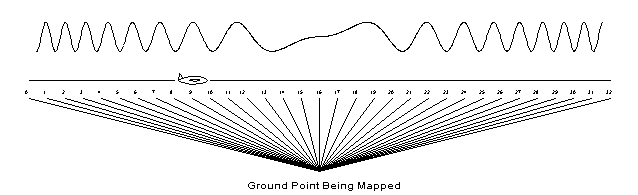
Note that the Doppler described here is "apparent" Doppler, not "instantaneous" Doppler (see Radar Doppler). For this reason, the SAR vehicle does not actually need to be moving when the measurements are being taken, but simply needs to be moved from one location to the next between measurements (not practical for an airplane, but very practical for a raised platform on a truck bed -- something which can be very useful in conserving budgetary funds during initial system testing).
The normal procedure for cross-correlation using Fourier transforms is to transform the time series data for each range bin into the frequency domain, multiply by the complex conjugate of the Fourier transform of the FM waveform for that range bin, and then inverse transform the data back into the time (x.y) domain. This procedure is complicated by the fact that the time-series data for a single range bin as defined on boresight (point 16 above) migrates through the range gate during successive PRI's due to the geometry of the flight path involved during the data collection process (notice how the range from the aircraft to the point of interest changes continually for successive points 0-32 above). The time series data cannot be easily corrected, because performing a correction for any one range bin would distort the data for all other range bins. However, the correction can be performed in the frequency domain, and surprisingly, in a very straightforward manner. A simple re-mapping of the freqency domain data prior to multiplication by the complex conjugate of the transform of the FM time history yields the desired result -- after, of course, the inverse transform has been performed and the complex points converted to power or log-power (see Real-Time Log Power Computation). The re-mapping amounts to a bending of the frequency-domain "hyperbola" into a straight line, such that all of the frequency-domain data corresponding to a particular range bin reside in a single array line:

This re-mapping is achieved by using the flight-path geometry to shift the Doppler bins from the extended ranges into a common range, as defined by the on-boresight point. This re-mapping does not involve any numerical operations on the frequency domain points, only a shifting of positions within the two-dimensional Range/Doppler array. For information on how to extend this procedure to more than one range bin in order to process the entire Range/Doppler array, see SAR Processing (One-Dimensional Fourier Transform, Multiple Range Bins) .For information on using interpolation to select points intermediate to those obtained from an evenly sampled data set, see Synthetic Aperture Radar (SAR) Processing Overview.